What are "Harmonic Overtones"?

Harmonic Overtones

Complex tones are periodic signals that consist of a fundamental frequency with associated harmonic overtones. These signals are, among other things, characteristic of musical instruments. In a musical context, overtones are referred to as harmonics or partials (even though partials are not always purely harmonic). The frequency of a tone is actually the frequency of the fundamental frequency.

The frequency of harmonic overtones is integer multiples of the frequency of the fundamental tone. If the frequency of the fundamental tone is 100 Hz, then the frequency of the second harmonic (second overtone) is 200 Hz, the third harmonic 300 Hz, the fourth harmonic 400 Hz, etc.

Besides frequency and magnitude, we also use phase to describe a complex tone. The phase component of a signal expresses how much a sinewave is delayed compared with a reference sinewave with the same frequency. The phase is only relevant if it is relative to a reference.

The phase is described by an angle (0⁰- 360⁰) as we also here refer to the unit-circle, a term from trigonometry. If two – same frequency –  sine waves are ‘in phase’, it means that there is no delay between them – the phase angle = 0⁰. If the two sines are ‘out of phase’ the phase angle is ≠ 0⁰; one is delayed compared to the other.

Sometimes the term ‘out of phase’ is misunderstood to mean two oppositely phased signals, one signal being an inverted version of the other. However, there is no delay between them. The phase angle is said to be 180⁰, or one signal has the inverted polarity of the other. On the input section of many mixing consoles, there is the Greek letter “Φ” (phi). This button inverts the input signal, so the polarity is swapped.

In general, when analyzing audio signals (or vibration signals), the frequency and the magnitude is called the ‘real part’ and the phase is called the ‘imaginary part’.


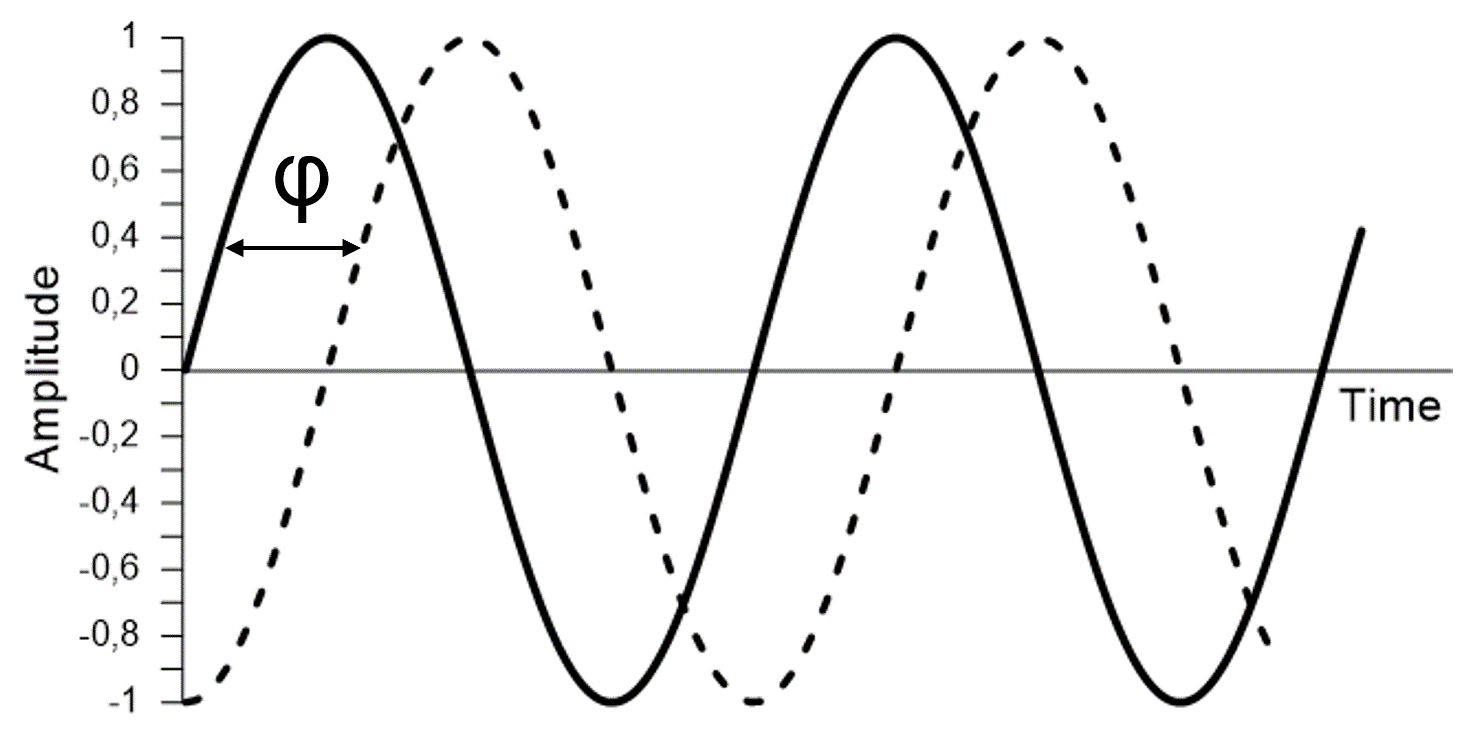
Figure 1. Phase is always relative to a reference.
 


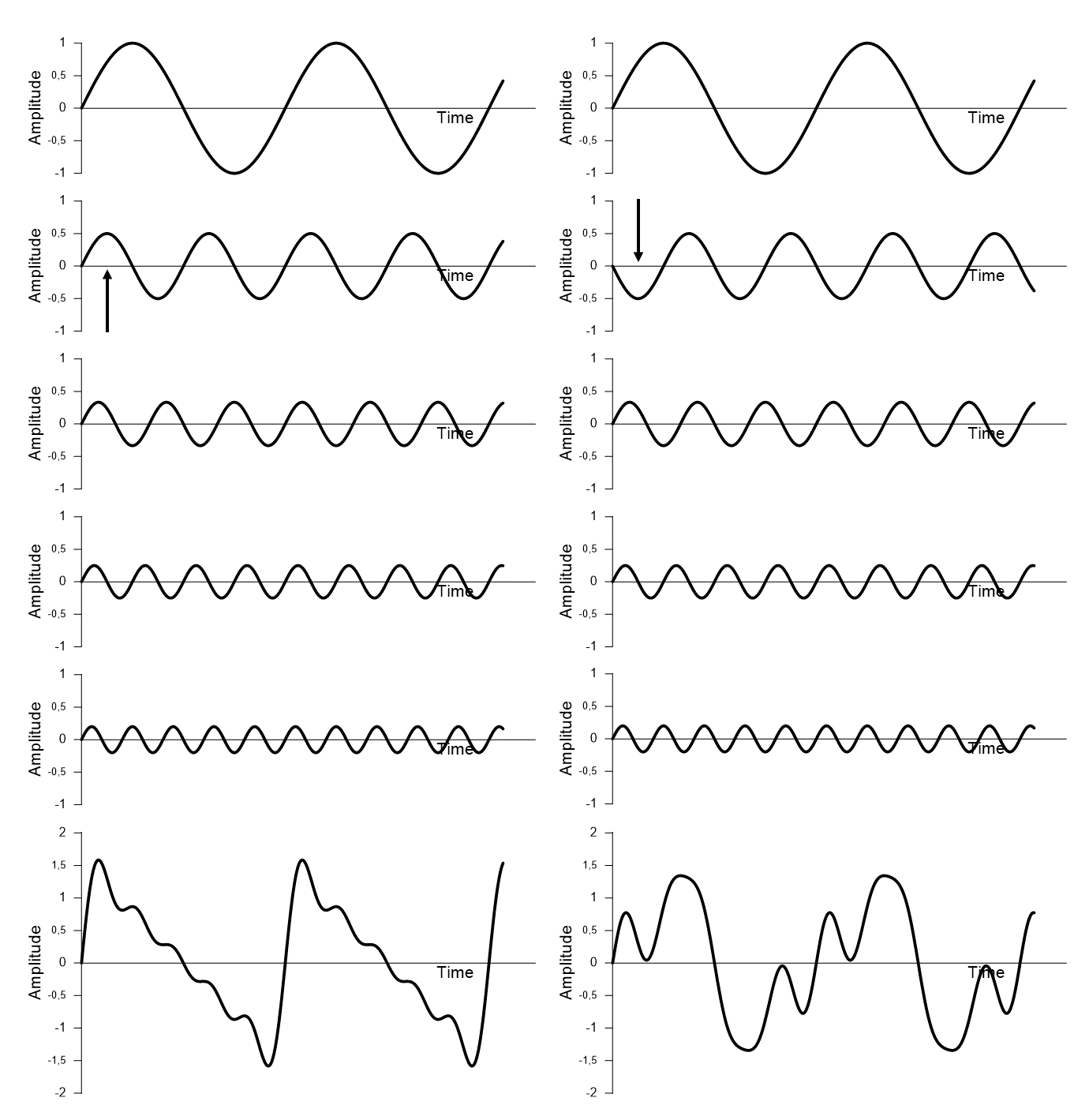
Figure 2. To the left five pure tones are shown, corresponding to a fundamental tone, the associated second harmonic overtone (with an amplitude = 1/2 ´ the fundamental tone), a third harmonic overtone (with an amplitude = 1/3 ´ the fundamental tone), a fourth harmonic overtone (amplitude = 1/4 ´ the fundamental tone), and a fifth harmonic overtone (amplitude = 1/5 ´ the fundamental tone). At the bottom, these five pure tones create a waveform that approximates a sawtooth waveform. Note that all the curves start at 0°. If the phase angles are different, then the resulting waveform would also have a different appearance, as shown to the right: A phase shift of 180⁰ is introduced to the 2^nd harmonic. Now the resulting waveform is different, despite the frequencies and their magnitudes are identical.
 

Special Waveforms
Among the periodic waveforms, there are characteristic waveforms such as a sinusoid, sawtooth, square, triangular, and pulse train (or pulse string).

The sawtooth wave contains the fundamental frequency and all harmonics in a specific proportion corresponding to the inverse of the number of the harmonic; (i.e., the 2^nd harmonic has ½ ´ amplitude of the fundamental, the 3^rd harmonic has 1/3 ´ amplitude of the fundamental frequency, and so on.). Further, all harmonics are added in phase; at waveform zero-crossings of the complex tone, all the individual harmonic tones are crossing zero as well (see fig 2).

The square wave contains the fundamental frequency and all the odd-numbered harmonics in the same declining proportion as the sawtooth wave. Further, as with the sawtooth wave, all harmonics are in phase.

The square wave is known from, among other places, electroacoustic equipment that is overloaded and thus ‘clips’ the peaks (positive and negative) of the waveform. Clipping is one way in which harmonic distortion can occur. The magnitudes of the harmonic overtones created are stated with reference to the fundamental frequency and quantified as a percentage of the fundamental (i.e., total harmonic distortion (THD) equals xx%).

The triangular wave contains the fundamental frequency and all the odd-numbered harmonics. However, the polarity of every second of the harmonics present (3^rd harmonic, 7^th harmonic, 11^th harmonic, and so on) is inverted. The decline of the level of the harmonics corresponds to the inverse square of the harmonic number (i.e., 1/9 ´ 3^rd harmonic, 1/25 ´ 5^th harmonic, 1/49 ´ 7^th harmonic, and so on).
 

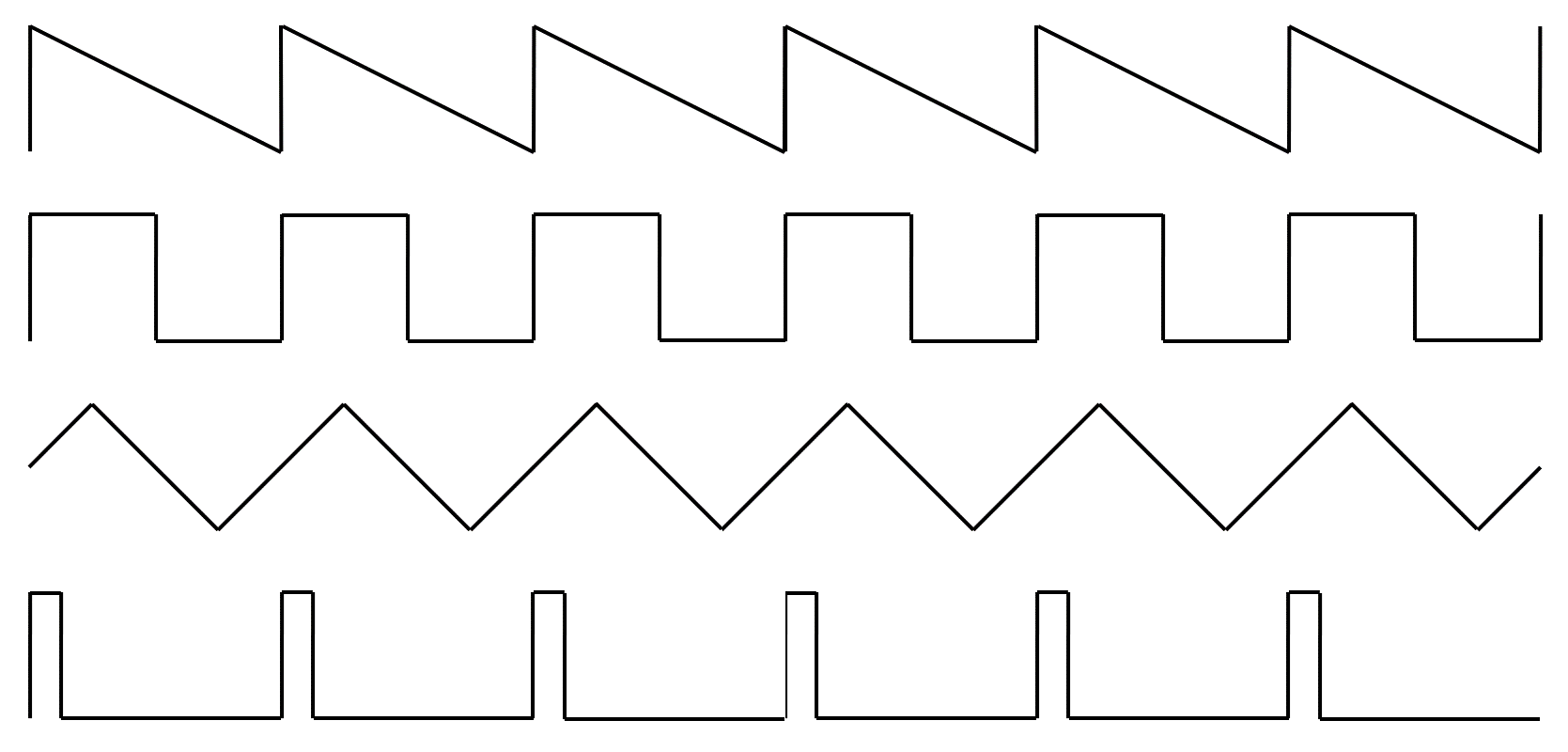
Figure 3. Special periodic, continuous waveforms: Sawtooth, square, triangular and pulse train.